Priority Queue

우선순위 큐를 구현하고 관련 문제를 풀어봅시다.

---

💡 우선순위 큐?

- Queue

큐(Queue)는 자료구조의 하나로 먼저 들어온 아이템이 먼저 나가는 First In First Out(FIFO) 선입선출 구조로 되어 있습니다.

- Priority Queue

우선순위 큐는 아이템마다 우선순위를 부여하여 우선순위에 따라 데이터 출력 방식을 결정하는 구조입니다.

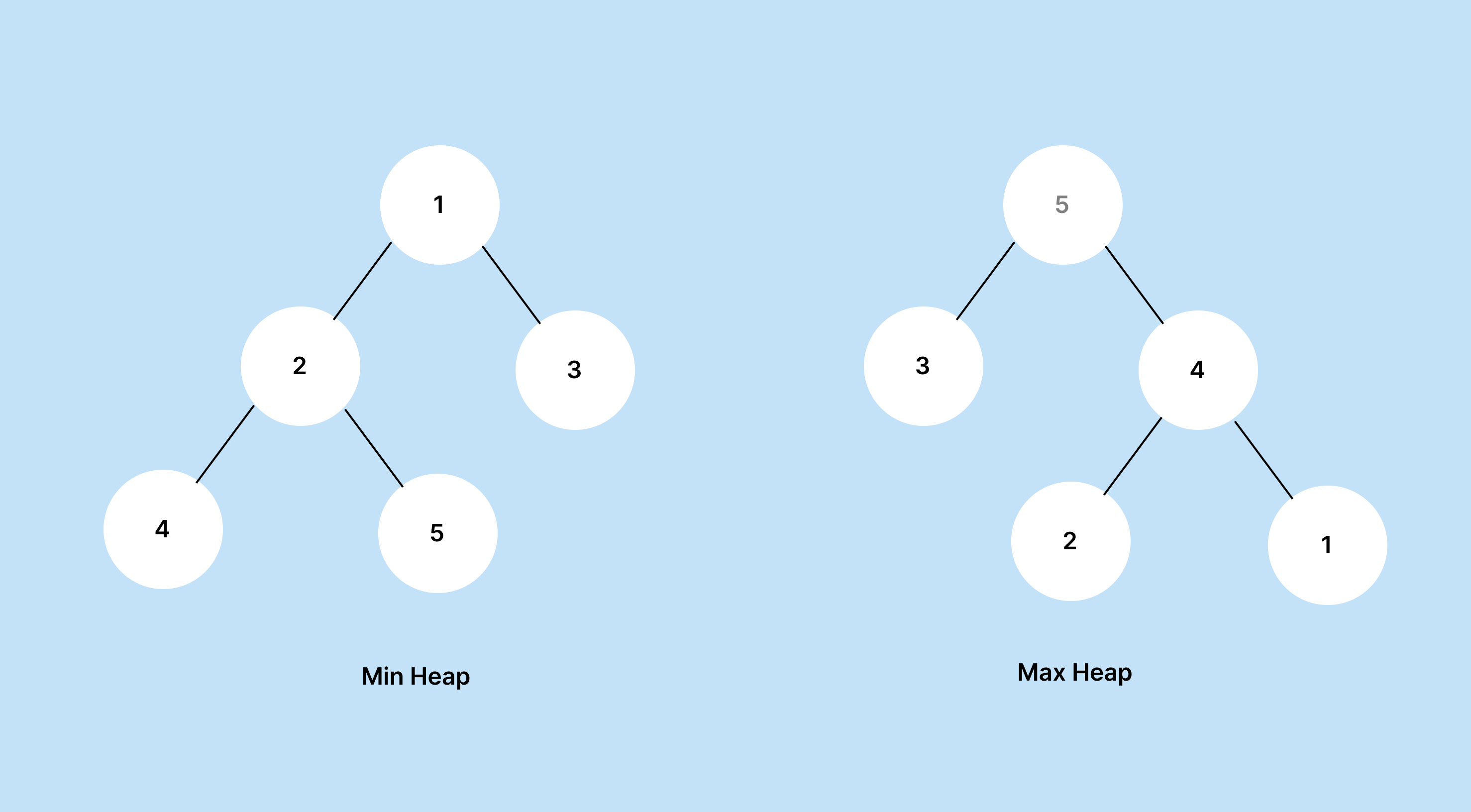
주로 우선순위 큐를 구현하기 위해서 힙 트리를 사용합니다.

힙은 여러 개의 값 중 가장 크거나 작은 값을 빠르게 찾아야 할 경우 사용됩니다.

일반적으로 트리 구조는 하나의 레벨마다 자식 노드의 수가 2배로 늘어나기 때문에 깊이가 H인 트리는 최대 2^H개의 노드가 있습니다.

반대로 말하면 N개의 노드의 트리 높이는 log₂N이기 때문에 시간 복잡도는 O(log₂N)입니다.

따라서 우선순위 큐를 사용하여 정렬 및 탐색 시간을 효과적으로 줄일 수 있습니다.

우선순위가 높은 아이템을 먼저 출력하는 Max heap과 낮은 아이템을 먼저 출력하는 Min Heap으로 나눌 수 있습니다.

우선순위 큐를 사용하는 예시에 대해서 알아보겠습니다.

---

💡 가운데를 말해요

백준 가운데를 말해요 문제

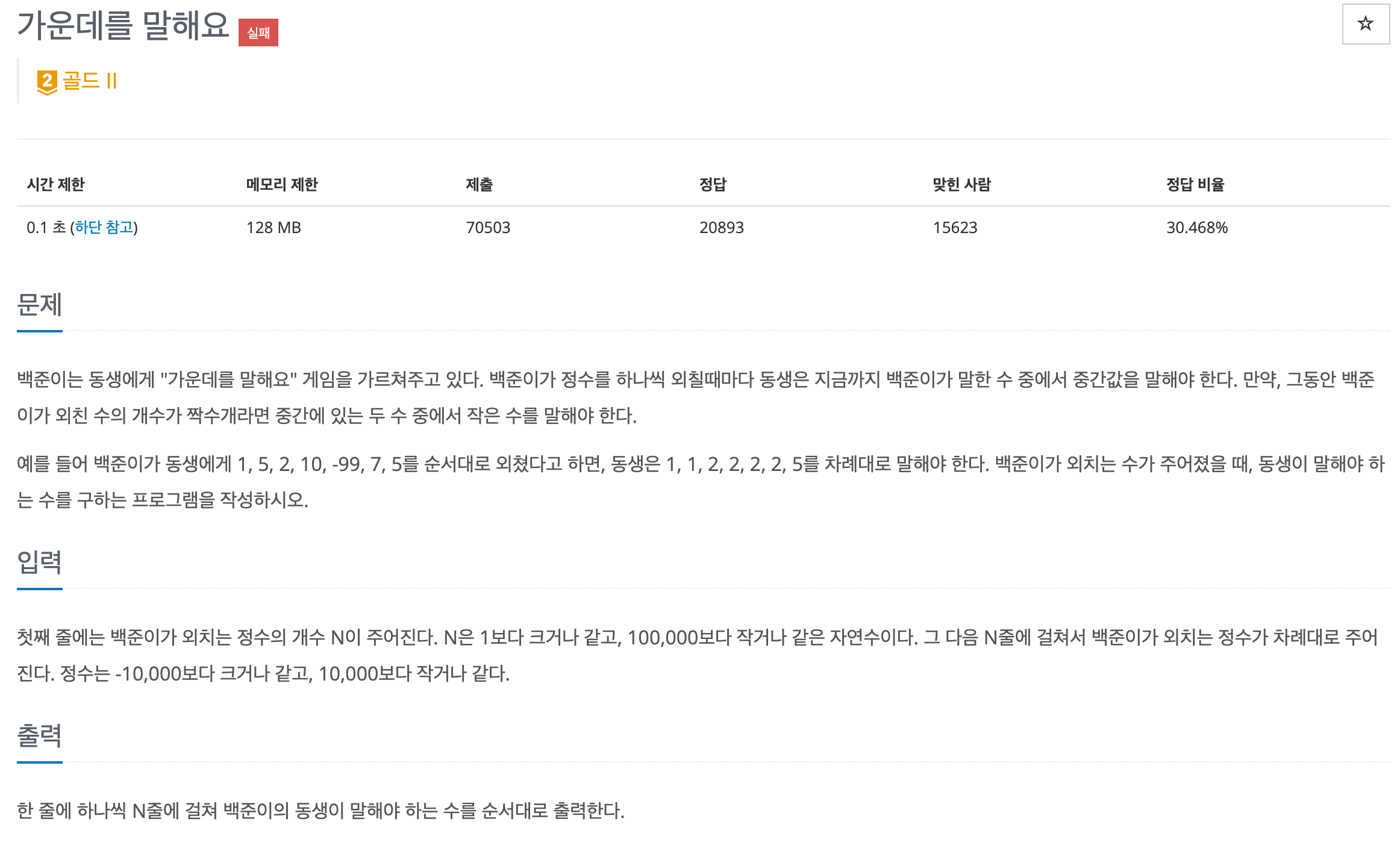
여러 개의 숫자를 받을 때마다 리스트에 넣고 가운데 값을 출력하는 문제입니다.

특이한 점은 시간제한이 0.1초 (파이썬 3은 0.6초)로 제한되어 있습니다.

- 우선순위 큐를 사용하지 않은 경우

먼저 자료구조 따위는 사용하지 않고 상남자처럼 구현해 보겠습니다.

1max_number = int(input())
2
3list = []
4
5for _ in range(max_number) :
6    list.append(int(input()))
7    list = sorted(list)
8
9    middle_index = len(list) // 2
10
11    if(len(list) % 2 == 0) : 
12        print(list[middle_index - 1])
13
14    else : 
15        print(list[middle_index])

의식의 흐름대로 가운데 수를 찾아갑니다.

시간초과로 실패했습니다.

어디서 시간을 많이 잡아먹는지 확인해 보겠습니다.

time 라이브러리를 사용하여 실행 시점의 시간을 측정할 수 있습니다.

1import time
2
3max_number = int(input())
4
5list = []
6
7for _ in range(max_number) :
8
9    list.append(int(input()))
10
11    # 시작 시간
12    start_time = time.time()
13
14    list = sorted(list)
15
16    # 정렬 시간
17    sort_time = time.time()
18
19    middle_index = len(list) // 2
20
21    if(len(list) % 2 == 0) : 
22        print(list[middle_index - 1])
23
24    else : 
25        print(list[middle_index])
26
27    # 끝난 시간
28    end_time = time.time()
29
30    print(f"Sort Time\t:\t{((sort_time - start_time) * 1000):.6f} ms")
31    print(f"Find Time\t:\t{((end_time - sort_time) * 1000):.6f} ms")
32    print(f"End Time\t:\t{((end_time - start_time) * 1000):.6f} ms")

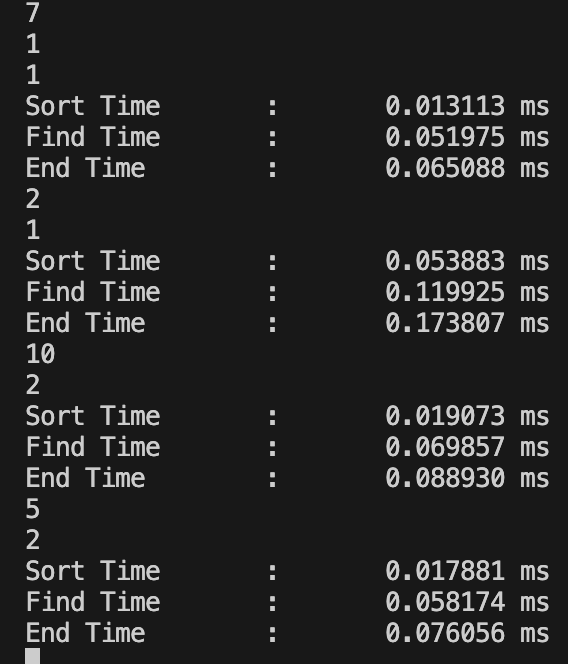
값을 넣고 중앙값을 찾아 출력하는데 약 0.1 ms가 소요되는 것을 알 수 있습니다.

특히 대부분의 시간을 중앙값을 찾는데 소요합니다.

문제에서 N은 최대 100,000이므로 최대 0.1 ms X 100,000 = 10초가 걸리는 것을 알 수 있습니다.

- 우선순위 큐를 사용한 경우

중앙값을 구하기 위해서는 먼저 정렬을 해야합니다.

문제를 풀기 전에 반대로 접근해 보겠습니다.

이미 정렬되어 있는 리스트가 있다고 가정해 보겠습니다.

정렬된 리스트에서 중앙값은 당연히 해당 리스트 길이의 절반에 해당하는 위치에 있습니다.

해당 리스트를 길이가 같은 2개의 리스트로 나눈다면 첫 번째 리스트의 마지막 값이 중앙값이 될 수 있습니다.

따라서 2개의 정렬된 리스트를 만들면 문제를 해결할 수 있습니다.

단, 두 번째 리스트의 값들은 첫 번째 리스트의 값보다 커야 합니다.

따라서 리스트는 정렬이 되어야 하며 마지막 값을 쉽게 꺼낼 수 있는 큐 형태가 적합합니다.

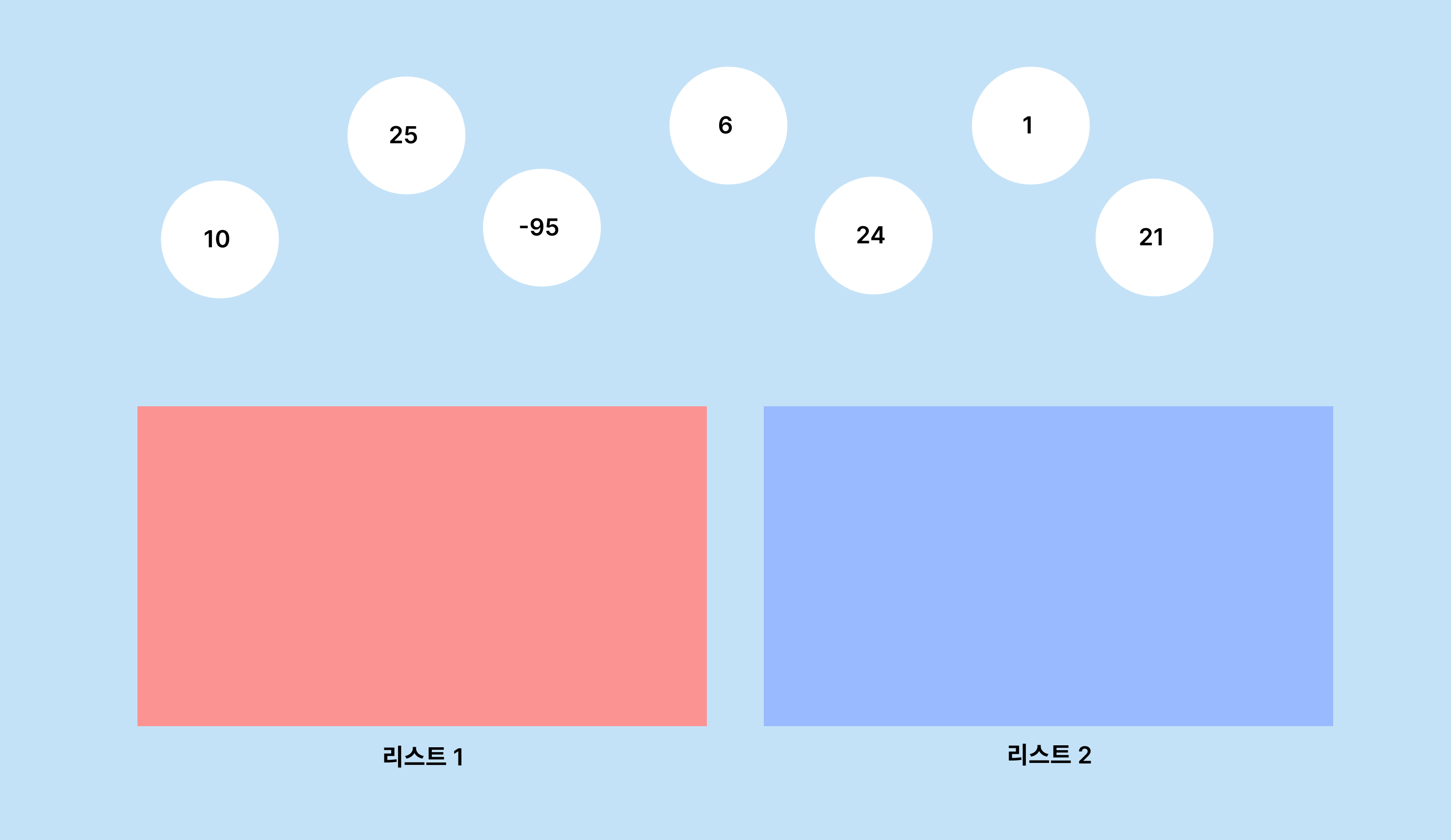
해당 방법을 사용해서 7개의 값 중에서 중앙값을 구해보겠습니다.

2개의 리스트를 만들어서 입력값을 넣을 수 있습니다.

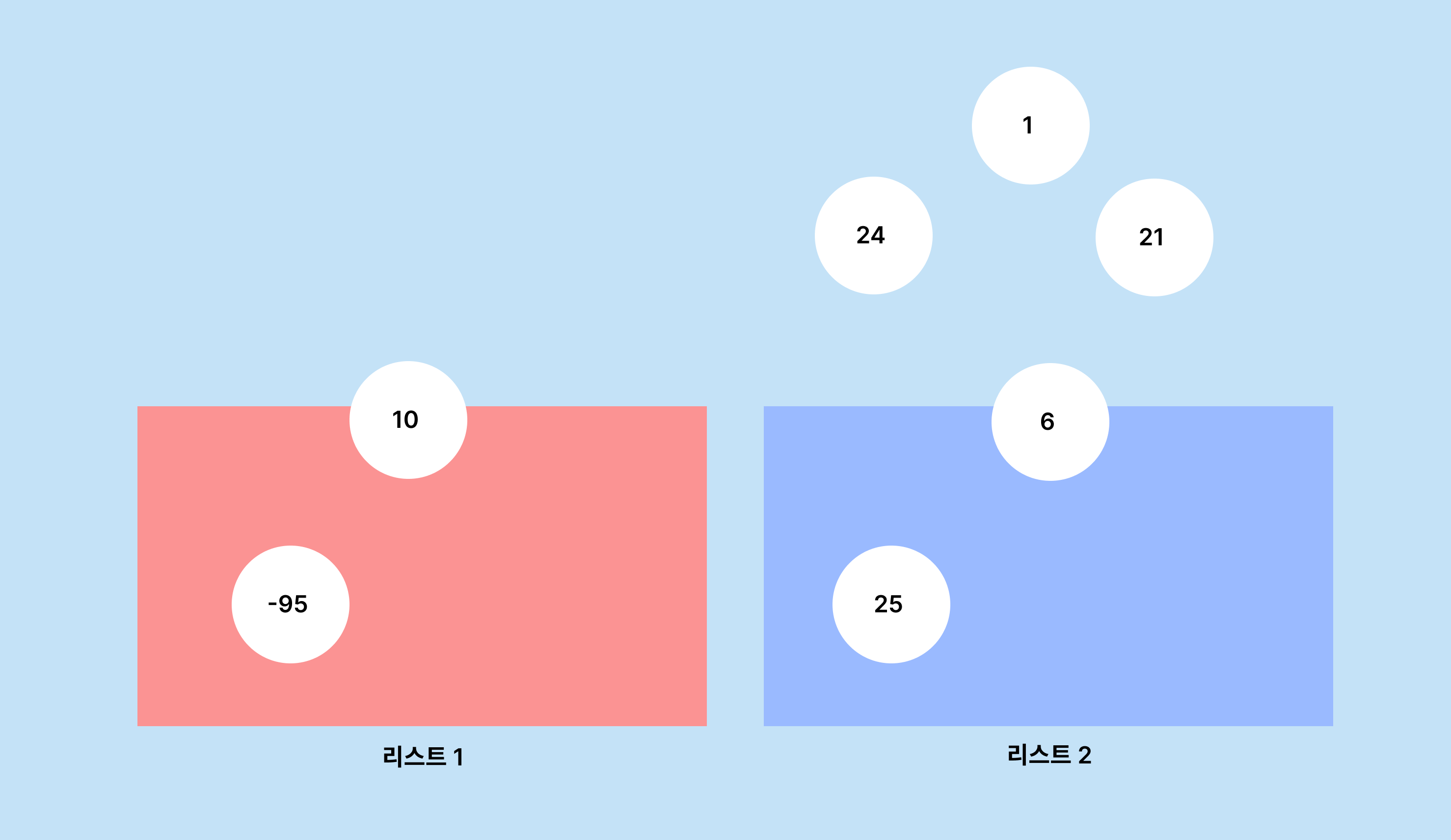
입력 순서대로 왼쪽 리스트부터 값을 채웁니다.

리스트에 들어온 아이템은 크기에 따라 정렬됩니다.

이때, 두 번째 리스트의 값이 반드시 첫 번째 리스트의 값보다 커야 합니다.

따라서 두 번째 리스트의 최소 값 > 첫 번째 리스트의 최대값입니다.

첫 번째 리스트는 값이 클수록 우선순위가 높게 설정하여 루트 값이 최대값이 되게합니다.

두 번째 리스트는 값이 작을수록 우선순위를 높게 설정하여 루트 값이 최소값이 되게합니다.

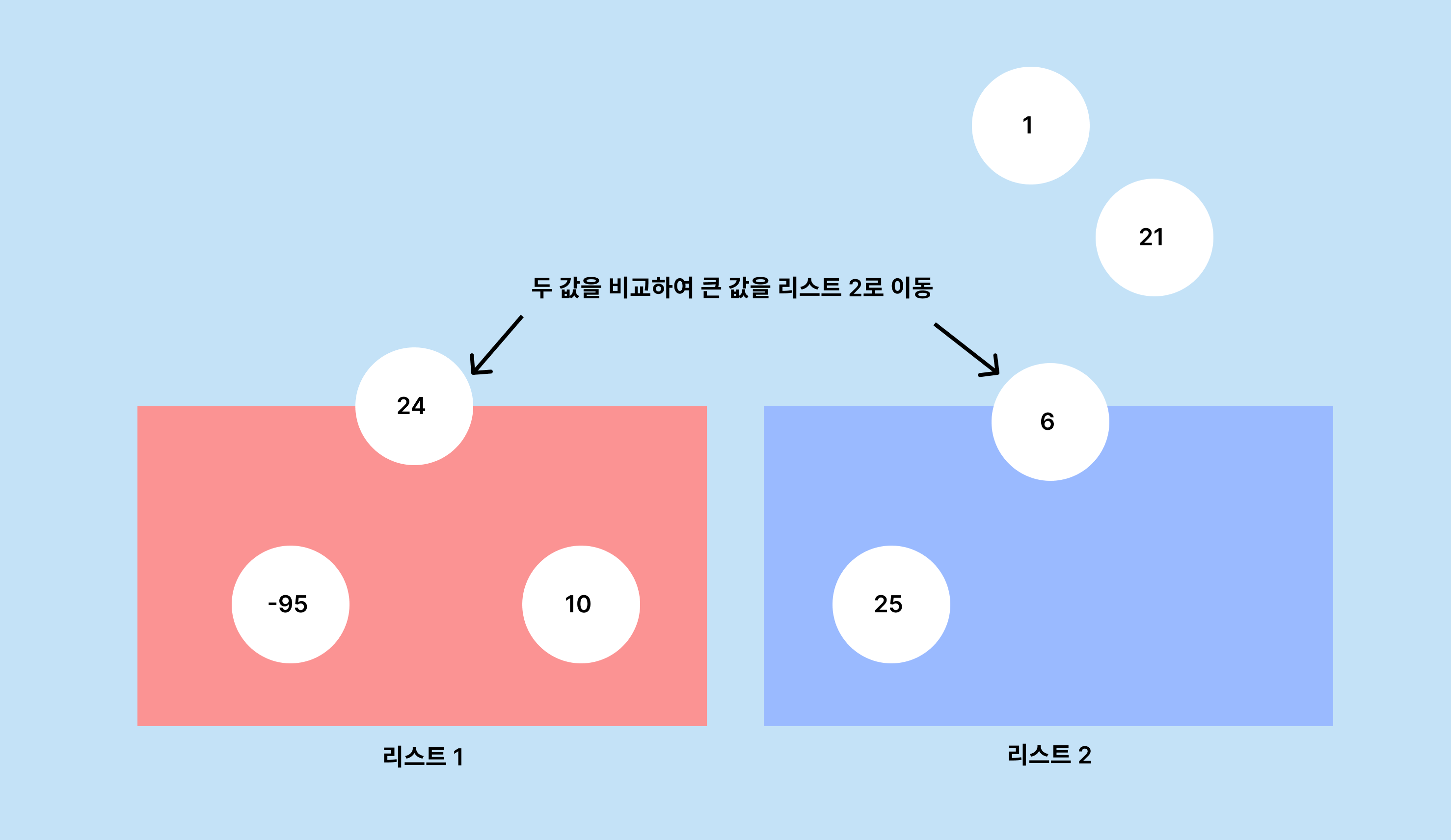
이렇게 하면 두 리스트의 값을 비교해서 빠르게 정렬할 수 있습니다.

이를 반복하면 두 리스트를 정렬할 수 있습니다.

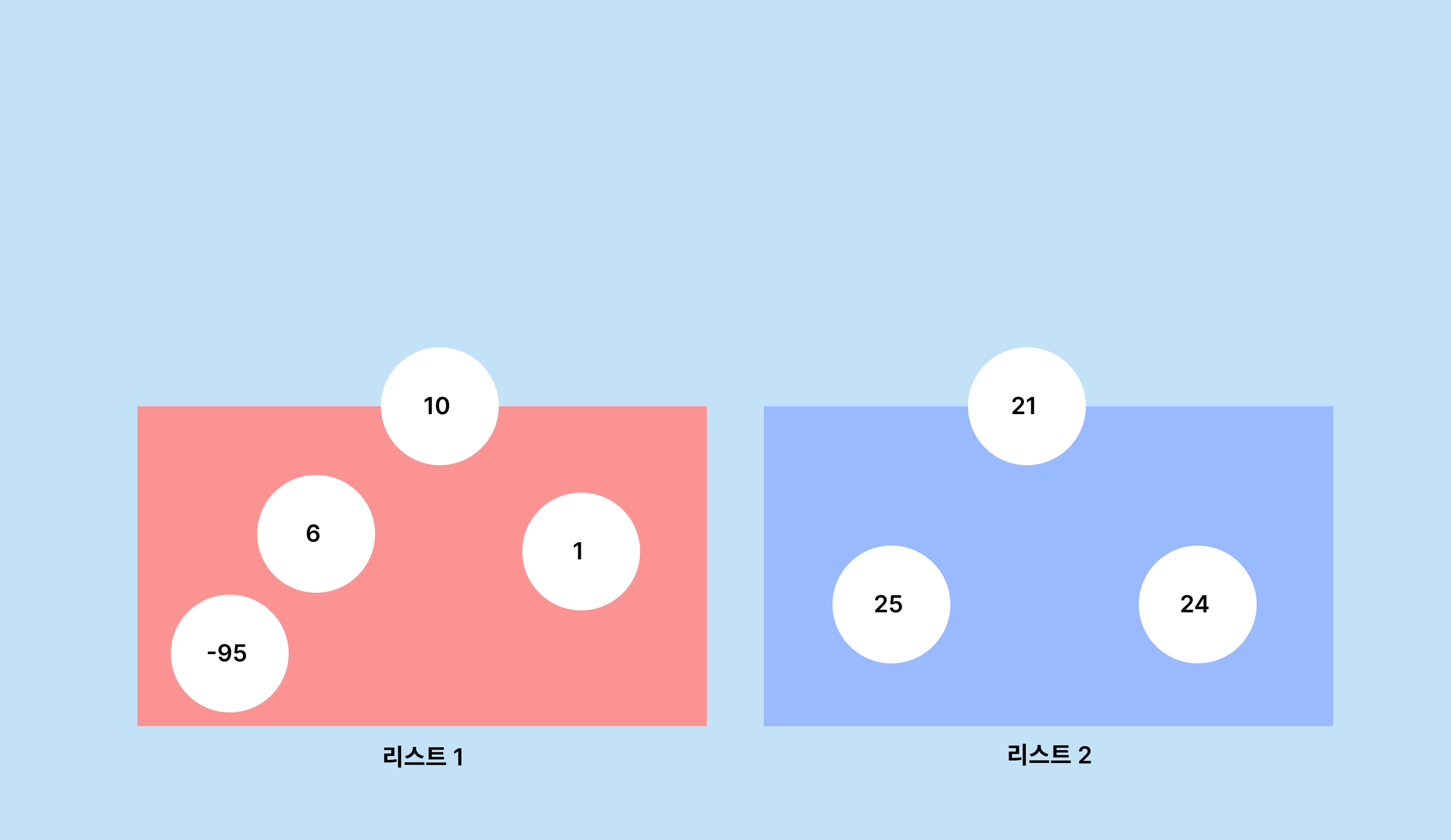
결과적으로 첫 번째 리스트의 루트 값이 중앙값이 됩니다.

코드로 확인해 보겠습니다.

파이썬은 우선순위 큐를 heapq 형태로 제공합니다.

min-heap만을 지원하기 때문에 max-heap을 구현하기 위해서는 아이템을 음수로 저장해야합니다.

1import heapq
2import sys
3import time
4
5input = sys.stdin.readline
6
7# 두 개의 힙을 사용합니다.
8max_heap = []  # 최대 힙 (중간값 이하의 값들을 저장)
9min_heap = []  # 최소 힙 (중간값 이상의 값들을 저장)
10
11N = int(input())
12for _ in range(N):
13    num = int(input())
14
15    start_time = time.time()
16
17    # 최대 힙과 최소 힙에 숫자를 적절하게 넣어줍니다.
18    if len(max_heap) == len(min_heap):
19        heapq.heappush(max_heap, -num)
20    else:
21        heapq.heappush(min_heap, num)
22
23    # 최대 힙의 최대값이 최소 힙의 최소값보다 크면 교환합니다.
24    if min_heap and -max_heap[0] > min_heap[0]:
25        max_value = -heapq.heappop(max_heap)
26        min_value = heapq.heappop(min_heap)
27        heapq.heappush(max_heap, -min_value)
28        heapq.heappush(min_heap, max_value)
29
30    end_time = time.time()
31
32    # 최대 힙의 루트 값이 중간값입니다.
33    print(-max_heap[0])
34
35    print(f"Time\t:\t{((end_time - start_time)):.6f} ms")

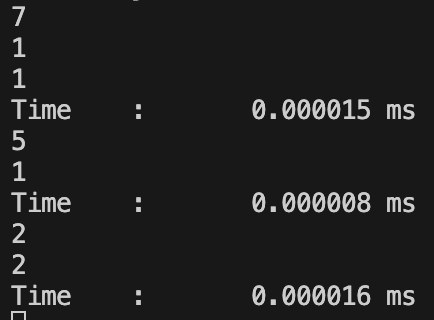
정렬과 탐색에 약 0.00001 ms가 소요되는 것을 확인할 수 있습니다.

---

💡 마무리

우선순위 큐를 사용하여 정렬과 탐색을 수행할 경우 자료구조를 사용하지 않았을 때보다 약 1,000배 빠른 것을 확인할 수 있었습니다.