DFS, BFS *미완성*
DFS, BFS에 대해서 알아봅시다.
2024년 11월 15일
by JISOO
0-1 Knapsack Problem
0-1 배낭 문제(0-1 Knapsack Problem)를 통해 동적 프로그래밍(DP)을 이해해 보겠습니다.
💡 배낭 문제?
배낭 문제는 몇 개의 물건이 무게(W)와 가치(V)를 지닐 때, 하나의 배낭에 최대 용량을 초과하지 않으면서 담을 수 있는 물건의 최대 가치를 구하는 문제입니다.
배낭 문제에는 Fraction Knapsack Problem, 0-1 Knapsack Problem이 있습니다.
물건을 쪼갤 수 있는 경우 Fraction, 없는 경우 0-1 문제로 나뉩니다.
배낭 문제는 동적 프로그래밍으로 접근할 수 있습니다.
💡 동적 프로그래밍(Dynamic Programming)
동적 프로그래밍(DP)은 복잡한 문제를 작은 문제로 나누어 해결하는 기법입니다.
가장 큰 특징으로는 이전의 계산을 기억(Memoization)합니다.
중복되는 계산이 필요하거나 최적화가 필요할 때 DP를 사용합니다.
예를 들어 피보나치 수를 계산할 때 5번째 피보나치를 구하려면
F(0) = 1
F(1) = 1
F(2) = F(0) + F(1) = 0 + 1 = 1
F(3) = F(1) + F(2) = 1 + 1 = 2
F(4) = F(2) + F(3) = 1 + 2 = 3
다음과 같이 F(4)의 결과를 얻기 위해서 F(2), F(3)의 결과 값을 구해야합니다.
이전 계산 결과가 저장되어 있지 않기 때문에 더 큰 값을 계산할수록 연산량이 늘어나는 문제가 발생합니다.
DP를 사용할 경우 값을 구할 때마다 해당 값을 저장할 수 있어 다음 연산에 사용하여 연산 속도를 높일 수 있습니다.
1cache = {} 2 3def fibo(n): 4if n == 0: return 0 5if n == 1: return 1 6 7 # 캐시에 값이 있다면 그 값을 사용 8 if n in cache: return cache[n] 9 10 # 캐시에 연산 결과를 저장 11 else: cache[n] = fibo(n - 1) + fibo(n - 2) 12 13 return cache[n]
💡 0-1 배낭 문제
배낭 문제에 해당하는 백준 12865번 문제입니다.
- 접근 방법
모든 물건을 비교해서 최적의 결과(최대 가치)를 구하는 문제입니다.
해당 배낭 문제는 다음 규칙이 있습니다.
- 물건은 쪼갤 수 없습니다. (부수면 안 됩니다.)
- 한번 사용한 물건은 다시 사용할 수 없습니다. (이미 가방에 들어갔기 때문)
물건을 쪼갤 수 없기 때문에 0-1 Knapsack 알고리즘에 해당합니다.
문제를 가볍게 생각한다면 물건을 넣느냐(1) 마느냐(0)의 문제입니다.
이 문제는 동적 프로그래밍을 사용하여 큰 문제를 작은 문제로 나눌 수 있습니다.
만약 허용량이 10인 배낭에 무게가 5인 물건을 넣었을 때, 허용량이 5인 배낭에 들어갈 수 있는 물건의 최대 가치를 구하는 문제와 동일해집니다.
DP를 통해 해결하기 위해서는 무게마다 최대 가치를 구해서 그 중 최대값을 구하면 되겠습니다.
- 코드 작성
전체 코드는 다음과 같습니다.
1# 물건의 개수, 배낭의 최대 허용량 2item_count, max_weight = map(int, input().split()) 3 4# 물건의 리스트 5data = [] 6 7# 물건은 (w,v) 형태로 저장합니다 8for _ in range(item_count): 9 w, v = map(int, input().split()) 10 data.append((w, v)) 11 12# 1차원 테이블을 형성합니다. 13dp = [0] * (max_weight + 1) 14 15# DP 16for w, v in data: 17 for i in range(max_weight, w - 1, -1): 18 dp[i] = max(dp[i], dp[i - w] + v) 19 20print(dp[max_weight])
물건을 등록하는 로직을 제외하고 핵심 로직만 알아보겠습니다.
1# 1차원 테이블을 형성합니다. 2dp = [0] * (max_weight + 1)
DP에서 중요한 점은 어떤 것을 기준으로 값을 저장하는지 생각해야 합니다.
문제에서 원하는 답은 허용할 수 있는 무게 중 최대 가치를 구하는 것이기 때문에 최대 무게를 기준으로 테이블을 형성할 수 있습니다.
코드상에서는 테이블이 곧 리스트이기 때문에 1차원 리스트를 생성합니다.
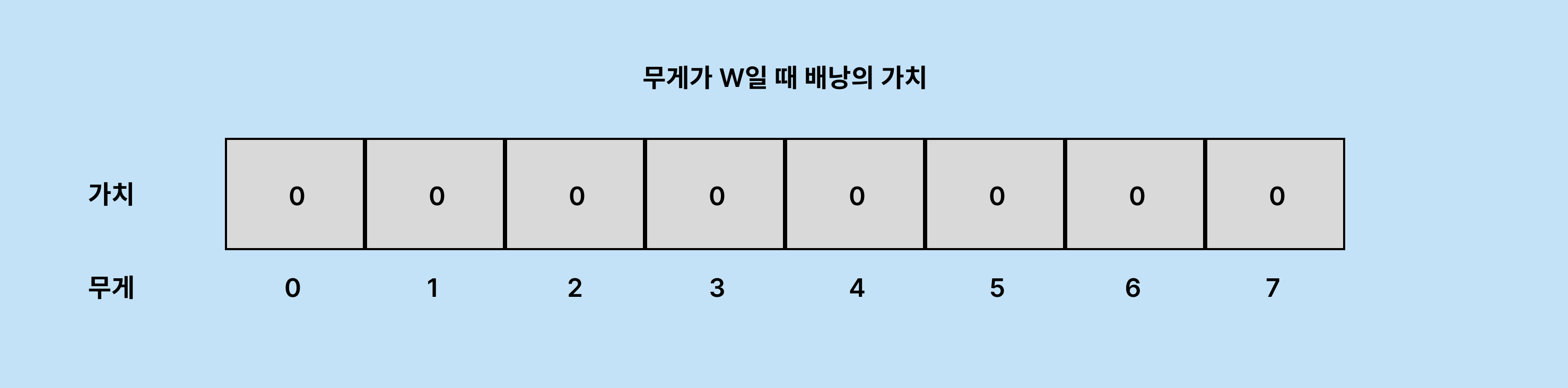
각 항목은 허용량이 W인 배낭의 최대 가치를 나타냅니다.
현재는 모두 0이 할당되어 있습니다.
최대 무게 이상의 경우 기록할 필요가 없기 때문에 최대 무게까지만 길이를 형성합니다.
1# DP 2for w, v in data: 3 for i in range(max_weight, w - 1, -1): 4 dp[i] = max(dp[i], dp[i - w] + v)
코드에서 가장 중요한 부분입니다.
잘게 쪼개서 설명하겠습니다.
1for w, v in data:
데이터에 입력된 순서대로 물건을 집어넣습니다.
연산 결과를 저장하기 때문에 순서는 상관이 없습니다.
1for i in range(max_weight, w - 1, -1):
이 때 물건의 무게 w가 max_weight보다 크다면 걸러집니다.
물건의 무게보다 가방의 허용량이 많아야 하므로 w-1까지의 경우만 구합니다.
최대값부터 거꾸로 계산한 이유는 물건은 한 번만 사용할 수 있기 때문입니다.
DP는 이전에 기록된 데이터를 사용하는데 순방향으로 계산할 경우 물건을 여러 번 사용하는 오류가 발생합니다.
이에 대해서는 밑에서 조금 더 설명하겠습니다.
1dp[i] = max(dp[i], dp[i - w] + v)
가장 중요한 공식입니다.
허용량이 W인 배낭에 무게가 N이고 가치가 K인 물건을 넣을 경우 남은 허용량은 W-N입니다.
따라서 허용량이 W-N인 배낭의 최대 가치를 구하여 K를 더할 경우 허용량이 W인 배낭의 최대 가치가 됩니다.
만약 순방향으로 계산할 경우를 가정하겠습니다.
1for i in range(w, max_weight + 1):
허용량 5인 배낭에 무게 2인 물건을 넣을 경우 DP 테이블은 다음과 같이 작성됩니다.
• i = 2일 때 : dp[2] = max(dp[2], dp[2 - 2] + 3)
• i = 3일 때 : dp[3] = max(dp[3], dp[3 - 2] + 3)
• i = 4일 때 : dp[4] = max(dp[4], dp[4 - 2] + 3) => 에러 발생
DP[4]를 계산할 때 DP[2]의 값을 사용하는데, 이때 이미 DP[2]의 값은 갱신되었기 때문에 물건을 한 번만 사용한다는 조건을 위반하게 됩니다.
따라서 역방향으로 DP 테이블을 순회하게 됩니다.
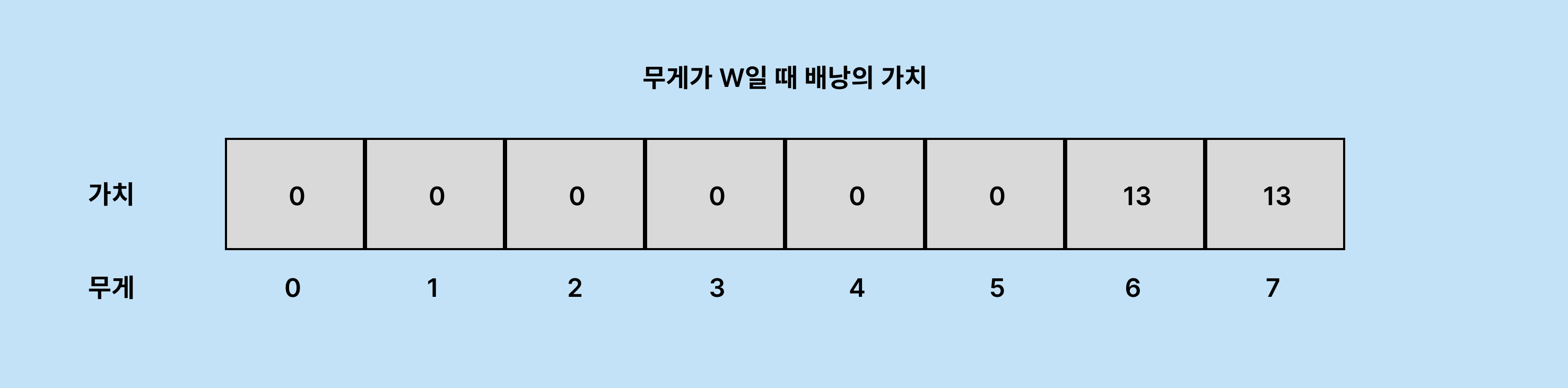
허용량 7의 배낭에 무게 6, 가치 13의 물건을 집었을 경우를 생각해 보겠습니다.
허용량 7의 배낭에 무게 6인 물건은 당연히 들어갈 수 있습니다.
현재 DP[7] 배낭의 최대 가치는 0입니다.
물건을 넣었을 때, 남은 배낭의 허용량은 1입니다.
따라서 허용량이 1인 배낭의 최대 가치와 물건의 가치 13을 더한 값과 DP[7] 배낭의 최대 가치를 비교하여 큰 값으로 갱신합니다.
DP[1] + 13 > DP[7] = 0 + 13 > 0이므로 13을 기록합니다.
DP[6]도 동일하게 처리합니다.
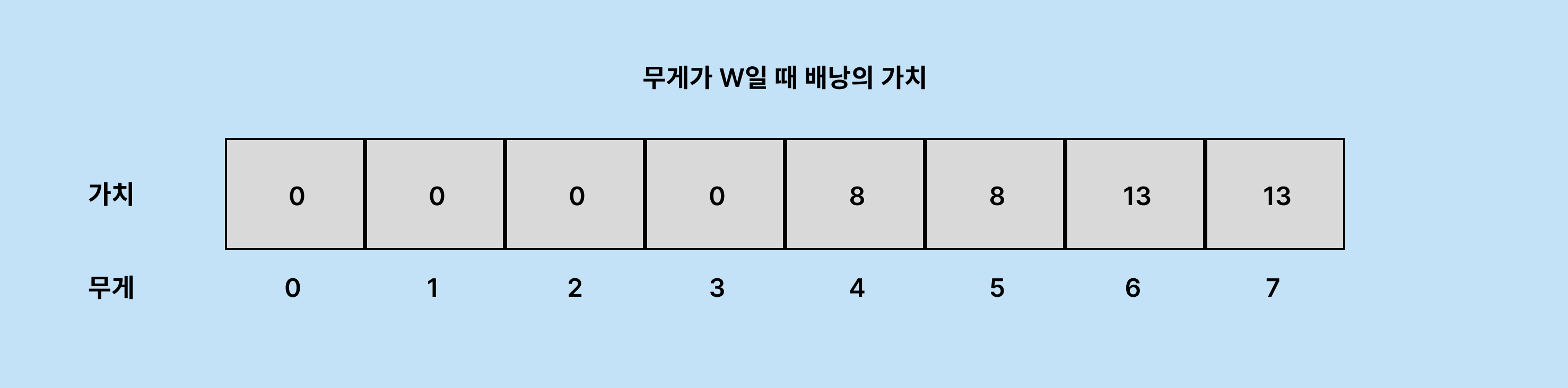
다음은 무게 4, 가치 8의 물건을 집었을 경우를 계산합니다.
허용량이 7인 배낭에서 무게 4의 물건을 넣을 경우 허용량 3인 배낭의 최대 가치를 구해야 합니다.
DP[3]은 아직 기록된 적이 없기 때문에 0 + 8 < 13 이므로 여전히 DP[7]의 최대 가치는 13입니다.
동일하게 처리해주면 DP[5], DP[4]는 최대 가치가 8이 됩니다.
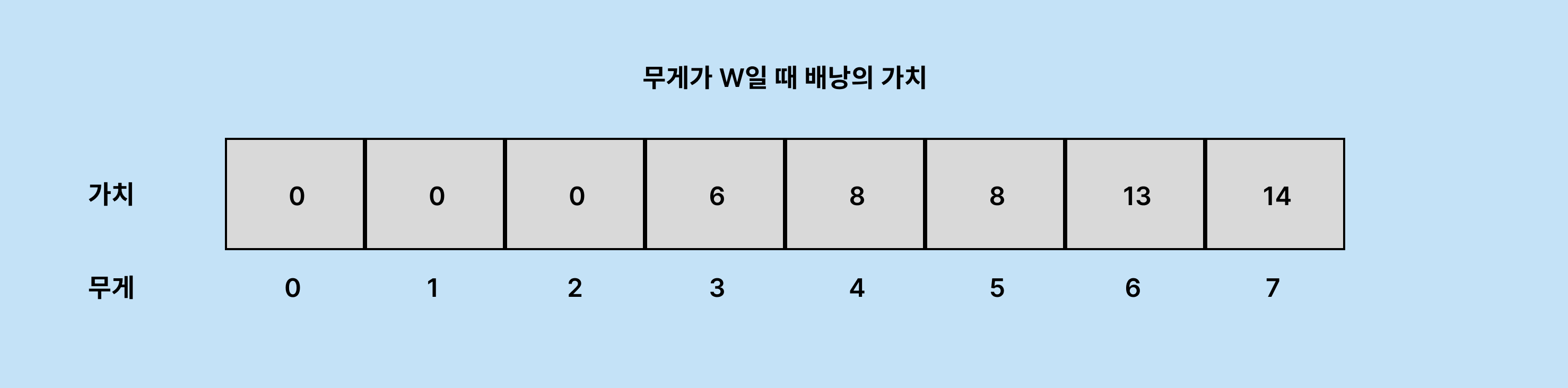
마지막으로 무게 3 가치 6의 물건을 집었을 경우를 가정하겠습니다.
허용량 7인 배낭에 무게 3의 물건을 넣었으므로 허용량 4인 배낭의 최대 가치를 구해야합니다.
이때 허용량 4인 배낭의 최대 가치는 8로 기록되어 있습니다.
8 + 6 > 13이므로 DP[7]의 최대 가치가 13에서 14로 갱신됩니다.
이를 반복하여 DP[7]에 허용량이 7인 배낭의 최대 가치를 구할 수 있습니다.
💡 마무리
배낭 문제를 통해 0-1 Knapsack 알고리즘과 DP에 대해서 알아보았습니다.
1